1, Teorema de Pitágoras.
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa ("el lado de mayor longitud del triángulo rectángulo") es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).Es muy importante llevar a la practica todo lo aprendido, por lo que una aplicación muy común del Teorema de Pitágoras, se da, al querer conocer la altura de un triángulo, el largo de un rectángulo, la longitud del lado de un cuadrado, y dado que en la vida cotidiana, nos podemos encontrar con elementos con las características de las figuras geometrícas antes mencionadas, el uso del teorema tiene una mayor aplicación y comprensión.
Ejemplo 1: Determinar el largo de un terreno rectangular, si el ancho del mismo es de 725 m y su diagonal mide 1005 m.
Solución:
Por lo que considerando la formula y según la figura, la incógnita es uno de los catetos, por lo que la fórmula queda de la siguiente manera:
b2=c2-a2
sustituyendo valores:
largo2 = 1,0052 - 7252
resolviendo:
largo2 = 1,010,025 - 525,625
largo2 = 484,400
y al obtener la raíz cuadrada, el largo del terreno tiene una magnitud de:
largo = 696 m
También puedes consultar Todo sobre el Teorema de Pitágoras
2.Teorema de Thales.
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:
De este teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si las rectas A, B, C son paralelas y cortan a otras dos rectas R y S, entonces los segmentos que determinan en ellas son proporcionales.
Una aplicación inmediata de este teorema sería la división de un segmento en partes iguales, o en partes proporcionales a números dados (con ayuda de compás, regla y escuadra o cartabón).
3. Problemas de escalas y maquetas.
4. Conceptos básicos de geometría.
Resumen Fórmulas de geometríaEjercicios propuestos. Geometría en el plano y en los cuerpos
Ejercicios propuestos. areas y volúmenes
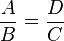
No hay comentarios:
Publicar un comentario